
...
The ANOVA Procedure.
What is the degrees of freedom for power and error?
See the answer. See the answer See the answer done loading. Given the following ANOVA table for three treatments each with six observations: Source. Sum of Squares. df. Mean square. Treatment. 1116.
How do you calculate error degrees of freedom from mean square?
What is the degrees of freedom treatment (between-group variation) of a completely randomized design (one-way) ANOVA test with 4 groups and 15 observations per each group? asked Sep 4, 2019 in Business by Catt819
How do you find the variance between treatments?
4. Analysis of variance is used to_____. A. compute a t test. B. simultaneously compare several population means. C. compare nominal data. D. compare population proportions. Simultaneously compare several population means. When testing differences between treatment means, the t statistic is based on ______. A. total degrees of freedom.
What if the difference between a pair of treatment means includes 0?
When comparing the mean annual incomes for executives with undergraduate and master's degrees or more,which of the following 95% confidence interval can be constructed? 2.0 ± 2.056 * 6.52 In a two-way ANOVA, the sources of variation are _______.
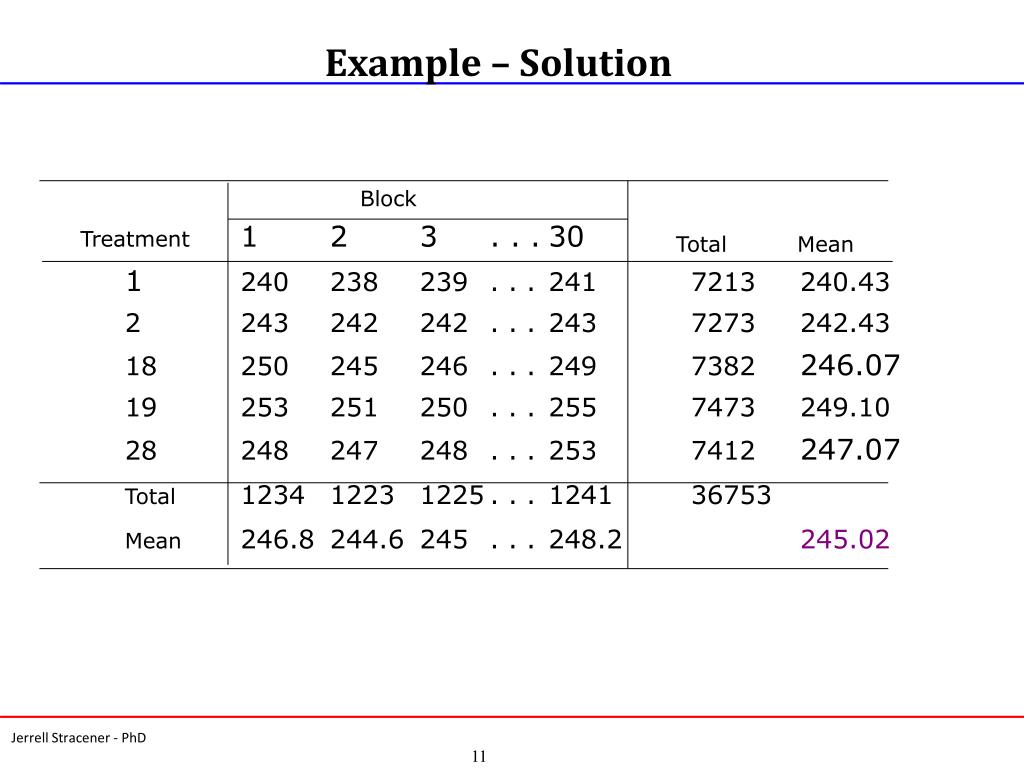
What are the degrees of freedom for the treatment?
The between treatment degrees of freedom is df1 = k-1. The error degrees of freedom is df2 = N - k. The total degrees of freedom is N-1 (and it is also true that (k-1) + (N-k) = N-1).
What is the degrees of freedom for error?
The mean squares are formed by dividing the sum of squares by the associated degrees of freedom. and the degrees of freedom for error are DFE = N - k \, . MSE = SSE / DFE . The test statistic, used in testing the equality of treatment means is: F = MST / MSE.
What is degree of freedom in variance?
For example, an estimate of the variance based on a sample size of 100 is based on more information than an estimate of the variance based on a sample size of 5. The degrees of freedom (df) of an estimate is the number of independent pieces of information on which the estimate is based.
How do you determine the degrees of freedom?
To calculate degrees of freedom, subtract the number of relations from the number of observations. For determining the degrees of freedom for a sample mean or average, you need to subtract one (1) from the number of observations, n.11 Jun 2021
What do degrees of freedom mean?
Degrees of freedom refers to the maximum number of logically independent values, which are values that have the freedom to vary, in the data sample.
What is degree of freedom with example?
So degrees of freedom for a set of three numbers is TWO. For example: if you wanted to find a confidence interval for a sample, degrees of freedom is n – 1. “N' can also be the number of classes or categories. See: Critical chi-square value for an example.
Is degrees of freedom N 1 or N 2?
This is a difference from before. As an over-simplification, you subtract one degree of freedom for each variable, and since there are 2 variables, the degrees of freedom are n-2.
How does degrees of freedom affect variance?
Therefore, the estimate of variance has 2−1=1 degree of freedom. If we had sampled 12 Martians, then our estimate of variance would have had 11 degrees of freedom. Therefore, the degrees of freedom of an estimate of variance is equal to N−1, where N is the number of observations.10 Jan 2021
What are the degrees of freedom for sample variance quizlet?
- For a sample of n scores the degrees of freedom for the sample variance are defined as df=n-1. - The degrees of freedom determine the number of scores in the sample that are independent and free to vary. The average value of the statistic is equal to the population parameter.
How do you find the degrees of freedom for an unequal variance?
To calculate degrees of freedom for ANOVA:Subtract 1 from the number of groups to find degrees of freedom between groups.Subtract the number of groups from the total number of subjects to find degrees of freedom within groups.Subtract 1 from the total number of subjects (values) to find total degrees of freedom.15 Feb 2022
How do you find the degrees of freedom between groups?
In other words, the degrees of freedom between groups is equal to the total number of groups minus one.12 Apr 2021
Analysis of Variance (ANOVA) Introduction
Earlier newsletters show how to compare two different processes or treatments. Many times you will want to compare more than two processes. ANOVA provides a method of doing this. In this newsletter, we will look at single factor ANOVA where we want to compare the results for different levels (treatments) of the factor.
Sum of Squares Calculations
The sum of squares calculations for the three sources in the ANOVA table are shown below. The information in the table below is helpful for the calculations.
Filling in the ANOVA Table
The rest of the ANOVA table can now be filled in. The ANOVA output from the software is shown below for this example.
Which Treatment Means are Different
The ANOVA table simply tells you that the treatment levels are significantly different. It doesn't tell you which ones are significantly different. More analysis is needed for this. One method is to create a scatter diagram. This chart from the software is shown below. The results are plotted versus power level.
Summary
This month we introduced the single factor ANOVA. This type of analysis is designed to determine if levels of a single factor impact a response variable. The ANOVA table was developed along with the calculations required. The scatter diagram and Box-Whisker plot were used to graphically show which levels could be different.
Quick Links
Thanks so much for reading our publication. We hope you find it informative and useful. Happy charting and may the data always support your position.
